コンピュータシミュレーション
コンピュータシミュレーションとは?
コンピュータシミュレーションは、現実の物理現象やシステムをコンピュータ上で模擬する技術です。 これにより、実際の実験や観測が難しい場合でも、様々な状況を再現し、分析や予測を行うことができます。 シミュレーションは、物理学、工学、経済学、生物学など、幅広い分野で利用されています。
シミュレーションの基本
シミュレーションは、以下の基本的なステップで行われます。
- モデル化: 対象となる現象やシステムを数学的なモデルで表現します。これには、物理法則や統計的な関係を用います。
- 数値化: モデルをコンピュータで扱える形式に変換します。これには、微分方程式の離散化や、確率分布の近似などが含まれます。
- 実行: シミュレーションを実行し、時間の経過に伴うシステムの挙動を計算します。これには、数値解析手法やアルゴリズムを使用します。
- 結果の解析: シミュレーションの結果を解析し、現象の理解や予測を行います。これには、グラフ化や統計的手法を用います。
倒立振子のシミュレーション
倒立振子のシミュレーションは、物理学や制御工学の基本的な問題であり、コンピュータシミュレーションの良い例です。 倒立振子は、棒が支点から逆さに立っている状態を指します。 いま、台車の上に棒を立てた次の倒立振子のモデルを考えます。
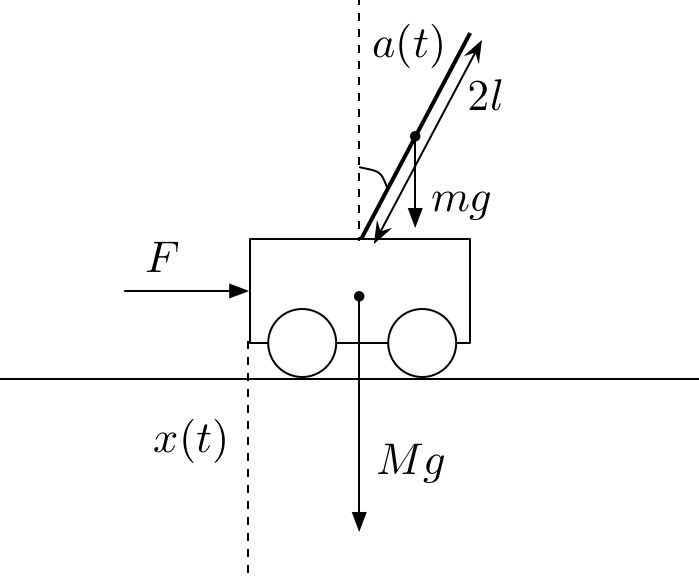
記号と意味
| 記号 | 意味 |
|---|---|
| $M$ | 台車の質量 |
| $m$ | 棒の質量 |
| $2l$ | 棒の長さ |
| $g$ | 重力加速度 |
| $F$ | 台車を押す力 |
| $x(t)$ | 台車の位置 |
| $a(t)$ | 棒の角度(垂直からの傾き) |
運動方程式
台車と棒の運動は次の式で表せます。
\[\begin{aligned} & (M + m) \ddot{x}(t) + m l^2 \ddot{a}(t) \cos a(t) = F + m l \dot{a}(t)^2 \sin a(t) \\ & m l \ddot{x}(t) \cos a(t) + m l^2 \ddot{a}(t) = m g l \sin a(t) \end{aligned}\]これを整理すると、次のように台車と棒の加速度が求まります。
\[\begin{aligned} & \ddot{x}(t) = \frac{F + l \dot{a}(t)^2 \sin a(t) - mg \sin a(t) \cos a(t)}{M + m \sin^2 a(t)} \\ & \ddot{a}(t) = \frac{(M+m) g \sin a(t) - (F + l \dot{a}(t)^2 \sin a(t)) \cos a(t)}{l (M + m \sin^2 a(t))} \end{aligned}\]シミュレーションの実行
これらの方程式を用いて、台車と棒の運動をシミュレーションすることができます。基本的なアイデアは、時間を少しずつ進めながら、台車の位置と棒の角度を更新していくことです。興味がある人は「オイラー法」や「ルンゲ・クッタ法」などの数値解析手法を調べてみてください。